In econometrics, time series analysis is essential for identifying trends, forecasting, and exploring relationships between variables. However, real-world economic and financial systems often experience sudden shifts caused by events like policy changes, economic crises, or technological advancements. These disruptions, known as structural breaks, can compromise the accuracy of time series models, leading to biased forecasts and unreliable conclusions if not properly accounted for.
Structural breaks pose significant challenges for models such as ARIMA, VAR, and GARCH. Addressing these challenges is critical for maintaining the validity of econometric analysis in fields like macroeconomics and finance. Detecting and managing structural breaks allows researchers to improve model accuracy and better understand dynamic economic systems.
What Are Structural Breaks?
Structural breaks refer to abrupt and significant changes in the underlying relationship between variables in a time series. These changes disrupt the consistency of the data-generating process, making models calibrated on pre-break data unsuitable for post-break analysis. Such changes are prevalent in economic and financial systems due to events like policy shifts, economic crises, or technological disruptions.
For example, consider the relationship between inflation and interest rates. A structural break might occur if a central bank transitions from targeting the money supply to targeting inflation, fundamentally altering how these variables interact. Similarly, an economic crisis can introduce breaks in GDP trends, employment rates, or market volatility.
Structural breaks are particularly critical in econometrics because they challenge one of the foundational assumptions of time series models—stationarity. Stationarity assumes that the statistical properties of a time series, such as its mean, variance, and covariance, remain constant over time. When a structural break occurs, these assumptions no longer hold, leading to several challenges:
Model Misspecification: Parameters estimated without accounting for breaks fail to represent the true relationships between variables.
Forecasting Errors: Models based on pre-break dynamics are often unreliable for predicting post-break periods.
Policy Misinterpretation: Policymakers relying on models that ignore breaks risk implementing ineffective or counterproductive measures.
Understanding and addressing structural breaks is essential for maintaining the reliability of econometric analyses and ensuring accurate insights from time series data.
Types of Structural Breaks
Structural breaks can be broadly categorized into three types: Level Breaks, Trend Breaks, and Volatility Breaks. Each type introduces unique challenges to time series analysis. The following illustration highlights these distinctions:
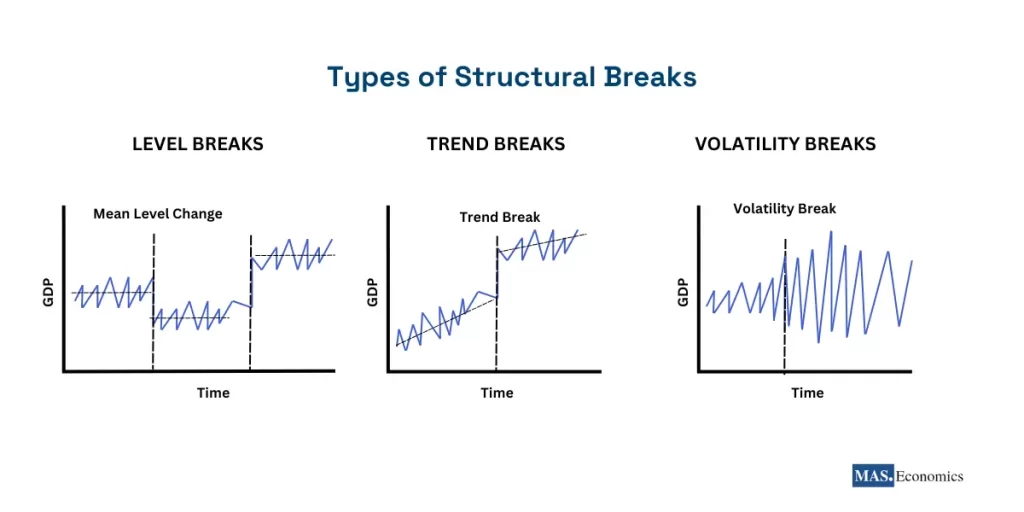
Level Breaks: Represent sudden shifts in the mean or baseline level of a series. For instance, a government stimulus program may abruptly increase GDP levels, creating a discontinuity in the data.
Trend Breaks: Indicate changes in the trajectory or growth rate of a series. An example is the productivity slowdown observed in advanced economies following the 2008 Global Financial Crisis.
Volatility Breaks: Reflect shifts in the variability or dispersion of a series. These are commonly seen during financial crises when market uncertainty spikes and price swings become more pronounced.
Real-World Examples
Structural breaks often arise from significant real-world events. Below are some examples highlighting their practical implications:
Policy Changes: The Federal Reserve’s adoption of inflation targeting in the 1990s introduced structural breaks in U.S. macroeconomic data, altering the relationships among interest rates, inflation, and unemployment.
Economic Crises: The 2008 Global Financial Crisis caused structural breaks in global GDP growth, unemployment rates, and financial market indices, disrupting long-established trends.
Technological Advancements: The rapid rise of e-commerce fundamentally altered traditional retail patterns, introducing structural breaks in consumer spending as businesses transitioned to online platforms.
By identifying and accounting for these breaks, econometricians can better adapt their models to reflect new economic realities, improving the accuracy of forecasts and the validity of policy recommendations.
Techniques for Detecting Structural Breaks
Detecting structural breaks is crucial for ensuring that econometric models remain reliable and relevant when the data-generating process changes. A variety of techniques have been developed to identify structural breaks, each suited for different scenarios. These methods help researchers pinpoint breakpoints and adjust their models accordingly.
The Chow Test
The Chow test is a foundational method used to detect a single structural break at a predefined point in time. It evaluates whether the coefficients of a regression model differ significantly before and after the suspected breakpoint.
How the Chow Test Works
-
Segment the Data: Divide the time series into two periods—before and after the suspected breakpoint.
-
Estimate Separate Regressions: Fit regression models for each segment and calculate their residual sum of squares (( RSS_1 ) and ( RSS_2 )).
-
Pooled Model: Estimate a single regression using the entire dataset and compute its residual sum of squares (( RSS_p )).
-
F-Test: Compare the segmented and pooled models using the F-statistic:
[
F = frac{(RSS_p – (RSS_1 + RSS_2))/k}{(RSS_1 + RSS_2)/(n – 2k)}
]
Where ( k ) is the number of parameters estimated, and ( n ) is the total number of observations.
Strengths and Limitations
- Strength: The Chow test is simple and intuitive, making it a widely used method in applied econometrics.
- Limitation: It requires prior knowledge of the breakpoint, which limits its applicability for exploratory analysis. Additionally, it cannot handle multiple structural breaks.
Example Application
The Chow test is often used to assess policy impacts. For instance, it can evaluate whether a tax reform caused a structural change in GDP by comparing pre- and post-reform periods.
The CUSUM Test
The Cumulative Sum (CUSUM) test is a dynamic method that detects structural breaks by analyzing the cumulative sum of residuals over time. Unlike the Chow test, it does not require pre-specified breakpoints, making it ideal for identifying unknown or gradual changes.
How the CUSUM Test Works
- Estimate Initial Parameters: Fit a regression model to the data and compute residuals.
- Calculate Cumulative Sums: Compute the cumulative sum of standardized residuals over time.
- Compare to Confidence Boundaries: Plot the cumulative sum against time. If the cumulative sum crosses predefined confidence boundaries, it indicates a structural break.
Strengths and Limitations
- Strength: The CUSUM test is well-suited for exploratory analysis and can detect gradual parameter changes.
- Limitation: It is sensitive to noise, which can lead to false positives in volatile datasets.
Example Application
The CUSUM test is commonly used in macroeconomic studies to detect changes in GDP growth rates following major reforms or shifts in trade policy.
The Bai-Perron Test
The Bai-Perron test is a sophisticated method designed to detect multiple structural breaks within a time series. It uses a global optimization algorithm to identify breakpoints and estimate parameters for each segment.
How the Bai-Perron Test Works
- Segment the Series: Identify potential breakpoints by minimizing residual variance across all possible segmentations.
- Estimate Parameters for Each Segment: Fit separate regressions for each segment to account for distinct dynamics.
- Optimize Breakpoint Placement: Adjust the placement of breakpoints to minimize overall residual variance.
Strengths and Limitations
- Strength: The Bai-Perron test handles multiple breakpoints simultaneously, making it ideal for analyzing long-term datasets with frequent shifts.
- Limitation: It is computationally intensive and requires significant processing power for large datasets.
Example Application
The Bai-Perron test is widely used in financial markets to analyze regime changes in volatility, such as identifying shifts during periods of economic expansion and contraction.
Comparing Detection Methods
| Method | Number of Breaks | Requires Known Breakpoint? | Key Strengths | Key Limitations |
|---|---|---|---|---|
| Chow Test | Single | Yes | Simple, intuitive | Limited to one break |
| CUSUM Test | Single/Unknown | No | Effective for gradual shifts | Sensitive to noise |
| Bai-Perron | Multiple | No | Handles multiple breaks | Computationally intensive |

|
||||
Impact on ARIMA, VAR, and GARCH Models
Structural breaks can significantly affect the reliability of popular econometric models like ARIMA, VAR, and GARCH. These models often assume stable relationships or dynamics over time, and ignoring structural breaks can lead to biased estimates, poor forecasts, and misleading inferences. Below, we explore the specific challenges and adjustments required for each model type.
Impact on ARIMA Models
Challenges Posed by Structural Breaks
ARIMA models are built on the assumption that the underlying time series is stationary or can be made stationary through differencing. Structural breaks disrupt this assumption by introducing abrupt changes in the mean, trend, or variance of the series. These breaks can result in:
- Overfitting: The model compensates for structural shifts by adding unnecessary parameters.
- Underfitting: The model fails to capture the changes, leading to inaccurate predictions.
For instance, during a major monetary policy shift, the inflation rate may experience a structural break, rendering pre-break ARIMA parameters irrelevant for post-break forecasting.
Adjusting ARIMA Models for Structural Breaks
To mitigate the impact of structural breaks, researchers often adopt a segmented analysis approach. This involves splitting the series into pre- and post-break periods and estimating separate ARIMA models for each segment. Additionally, diagnostic tests like the Augmented Dickey-Fuller (ADF) test, modified to account for breaks, are used to identify non-stationary segments.
For example, during a shift in fiscal policy, forecasting GDP accurately would require separate models for the pre-policy and post-policy periods to account for the distinct dynamics in each regime.
Impact on VAR Models
Challenges in Modeling Interdependencies
VAR models analyze interdependencies among multiple variables, treating each as endogenous. Structural breaks introduce instability in these relationships, resulting in:
- Parameter Instability: Shifting relationships between variables undermine the reliability of model estimates.
- Impulse Response Function Errors: The estimated impact of shocks becomes unreliable as structural breaks distort the interdependencies.
For instance, if a structural break alters the relationship between GDP, inflation, and interest rates, the VAR model may fail to provide meaningful insights into the economy’s response to monetary policy shocks.
Addressing Structural Breaks in VAR Models
To adjust for structural breaks, researchers often incorporate dummy variables that capture the effects of breaks, allowing the model to differentiate between pre- and post-break dynamics. Alternatively, regime-switching VAR models adapt parameters to reflect distinct economic regimes.
Another effective approach is to estimate separate VAR models for each regime. For example, analyzing the effects of a fiscal stimulus might involve estimating one VAR model for the pre-stimulus period and another for the post-stimulus period to capture the structural shift in fiscal policy dynamics.
Impact on GARCH Models
Volatility Misestimation Due to Structural Breaks
GARCH models are widely used to analyze financial time series, particularly for volatility forecasting. Structural breaks in volatility regimes—common during financial crises—can distort the model’s ability to accurately capture volatility clustering. These breaks may lead the model to:
- Misinterpret Regime Changes: Abrupt shifts in variance are often incorrectly attributed to long-term persistence.
- Overestimate or Underestimate Volatility: The model fails to account for sudden spikes or declines in market uncertainty.
For instance, during the 2008 Global Financial Crisis, a structural break caused a sudden spike in market volatility, which GARCH models might misinterpret as persistent volatility rather than a regime-specific event.
Adapting GARCH Models to Structural Breaks
To address these challenges, researchers adopt regime-switching GARCH models that explicitly account for structural breaks by allowing distinct volatility regimes in pre- and post-break periods. Another approach involves recalibrating GARCH parameters after detecting a break to ensure alignment with the updated volatility structure.
For example, analyzing stock market volatility during a financial crisis might require separate GARCH models for the pre-crisis and crisis periods to accurately capture the heightened uncertainty and subsequent stabilization.
Practical Applications in Macroeconomics and Finance
Structural breaks are not just theoretical challenges; they have profound implications for analyzing economic and financial systems. By identifying and addressing these breaks, researchers and policymakers can refine their models, enhance forecasting accuracy, and make more informed decisions. Below are key areas where structural breaks play a pivotal role.
Macroeconomic Policy Analysis
Structural breaks are particularly relevant when analyzing the impact of significant shifts in monetary or fiscal policy. For instance, a central bank transitioning from targeting money supply to inflation targeting introduces a structural break in the relationships between key macroeconomic variables like interest rates, inflation, and GDP.
Importance of Adjusting for Breaks
Failing to account for these breaks can lead to flawed inferences about policy effectiveness. Models calibrated on pre-break dynamics often misrepresent the relationships between variables, producing misleading forecasts and policy recommendations.
Application Example
Consider a fiscal stimulus program designed to boost GDP growth. The program may alter private sector investment and consumption patterns, creating distinct dynamics in pre-stimulus and post-stimulus periods. Segmenting the data around the stimulus implementation allows researchers to capture these regime-specific effects, helping policymakers understand how the program interacts with other economic variables like employment and inflation.
Financial Market Volatility
In financial markets, structural breaks often coincide with crises, regulatory changes, or major geopolitical events. These events introduce abrupt shifts in market dynamics, making structural break detection essential for accurate risk assessment and investment strategy development.
Handling Breaks in Volatility
Volatility models that fail to account for structural breaks risk overestimating or underestimating market uncertainty. Regime-switching GARCH models and other break-adjusted volatility frameworks allow analysts to differentiate between periods of high and low volatility.
Application Example
During the 2008 Global Financial Crisis, structural breaks caused sudden spikes in credit spreads, bond yields, and stock market volatility. Adjusting for these breaks enabled investors to refine their portfolios, hedge risks effectively, and adapt to changing market conditions. Similarly, detecting structural breaks in market indices helped analysts improve their forecasts and respond proactively to future crises.
Time Series Forecasting
Structural breaks pose significant challenges for time series forecasting, particularly when external shocks, such as policy changes or economic crises, alter the underlying data-generating process. Models that fail to account for these breaks often produce unreliable predictions, hindering decision-making for businesses and policymakers.
Adapting Forecasting Frameworks
Incorporating structural break detection into forecasting frameworks involves recalibrating models to reflect regime-specific dynamics. For example, during a period of carbon tax implementation, forecasting energy demand requires splitting the data into pre- and post-tax periods to capture behavioral shifts introduced by the policy. This adjustment enhances forecast accuracy and provides actionable insights.
Sector-Specific Applications
Structural breaks also have sector-specific implications, particularly in industries subject to rapid technological change, regulatory shifts, or external shocks:
Labor Markets: Policy changes, such as increases in the minimum wage or labor law reforms, create structural breaks that significantly affect employment trends and wage dynamics.d adapt to changes in market conditions or macroeconomic environments.
Retail and E-Commerce: The rise of online shopping introduced structural breaks in consumer spending patterns, requiring updated demand forecasting models to account for the shift from physical stores to digital platforms.
Energy Economics: Volatility in oil prices caused by geopolitical tensions or supply chain disruptions introduces structural breaks in pricing models, investment planning, and policy analysis.
Conclusion
Structural breaks are a significant factor in time series analysis, highlighting the need for models that can adapt to sudden changes in data-generating processes. Properly identifying and addressing these breaks enhances the accuracy of forecasts and the reliability of econometric models, offering clearer insights into dynamic economic and financial systems.
Techniques such as the Chow test, CUSUM, and Bai-Perron test are critical for detecting and managing structural breaks. Their application ensures that models like ARIMA and GARCH remain robust when faced with events such as policy changes or economic crises, maintaining the validity of time series analysis in complex scenarios.
FAQs:
What are structural breaks in time series analysis?
Structural breaks are abrupt changes in the underlying relationship between variables in a time series, caused by events like policy changes, economic crises, or technological advancements. These breaks disrupt the consistency of the data-generating process.
Why are structural breaks significant in econometrics?
Structural breaks are significant because they violate stationarity assumptions, leading to biased estimates, unreliable forecasts, and misinformed policy decisions if not accounted for in time series models.
How can structural breaks be detected?
Structural breaks can be detected using methods such as the Chow test for predefined breakpoints, the CUSUM test for unknown or gradual changes, and the Bai-Perron test for identifying multiple breakpoints in a dataset.
What is the impact of structural breaks on time series models?
Structural breaks affect the accuracy of models like ARIMA, VAR, and GARCH by introducing parameter instability and misrepresenting trends or volatility patterns, resulting in unreliable predictions and analysis.
How are structural breaks managed in econometric analysis?
Structural breaks are managed by segmenting data into pre- and post-break periods, incorporating dummy variables, or using regime-switching models to account for distinct dynamics across different time periods.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics
















