Regression analysis is a cornerstone of econometrics, widely used to model relationships between variables. Traditional methods like Ordinary Least Squares (OLS) estimate the conditional mean of the dependent variable based on independent variables. While effective for capturing average relationships, OLS assumes a uniform relationship across the entire distribution, which may not accurately reflect real-world data patterns.
Quantile regression provides a more detailed approach by modeling different points, or quantiles, of the conditional distribution. This technique uncovers how relationships between variables vary across the distribution, making it invaluable for studying heterogeneity. Applications include analyzing income inequality, extreme healthcare costs, or financial risk profiles. Unlike OLS, which focuses on average effects, quantile regression examines effects at various percentiles, offering a deeper and more comprehensive understanding of the data.
With its ability to handle outliers, accommodate heteroskedasticity, and provide insights beyond the mean, quantile regression has become a critical tool in econometrics. Its flexibility and robustness make it well-suited for addressing complex data challenges and uncovering nuanced relationships.
How Quantile Regression Differs from OLS
Regression analysis forms the backbone of econometric modeling, offering tools to analyze relationships between variables. Among these tools, Ordinary Least Squares (OLS) is the most commonly used due to its simplicity, computational efficiency, and interpretability. However, OLS primarily focuses on estimating the conditional mean of the dependent variable, making it suitable for analyzing “average” effects.
While useful, this approach has inherent limitations when the data exhibits heterogeneity or skewness. For instance, OLS assumes that the relationship between the independent variables and the dependent variable remains constant across the entire distribution of the dependent variable. But what happens when this assumption doesn’t hold? This is where quantile regression comes into play, offering a richer and more flexible alternative to OLS.
Quantile regression, developed by Koenker and Bassett in 1978, extends the regression framework by modeling different quantiles (e.g., median, lower quartile, upper quartile) of the conditional distribution of the dependent variable. By shifting the focus from the mean to specific quantiles, quantile regression provides insights into how independent variables influence different parts of the distribution, unveiling relationships that OLS might overlook.
How Quantile Regression Differs from OLS
Regression analysis forms the backbone of econometric modeling, offering tools to analyze relationships between variables. Among these tools, Ordinary Least Squares (OLS) is the most commonly used due to its simplicity, computational efficiency, and interpretability. However, OLS primarily focuses on estimating the conditional mean of the dependent variable, making it suitable for analyzing “average” effects.
While useful, this approach has inherent limitations when the data exhibits heterogeneity or skewness. For instance, OLS assumes that the relationship between the independent variables and the dependent variable remains constant across the entire distribution of the dependent variable. But what happens when this assumption doesn’t hold? This is where quantile regression comes into play, offering a richer and more flexible alternative to OLS.
Shifting the Focus: Beyond the Mean
Quantile regression, introduced by Koenker and Bassett in 1978, extends the regression framework by estimating conditional quantiles instead of the conditional mean. This allows researchers to explore how the effects of independent variables vary across different parts of the dependent variable’s distribution. For instance, in a study on wages, quantile regression can reveal how factors like education influence income at the 25th percentile (low-income earners), the median (middle-income earners), and the 90th percentile (high-income earners). Such insights are invaluable in understanding heterogeneity in data that OLS might obscure.
The illustration below demonstrates the difference between OLS and quantile regression. While OLS estimates the average relationship across the entire dataset, quantile regression models specific points (or quantiles) in the conditional distribution, providing a more detailed picture of variable relationships.
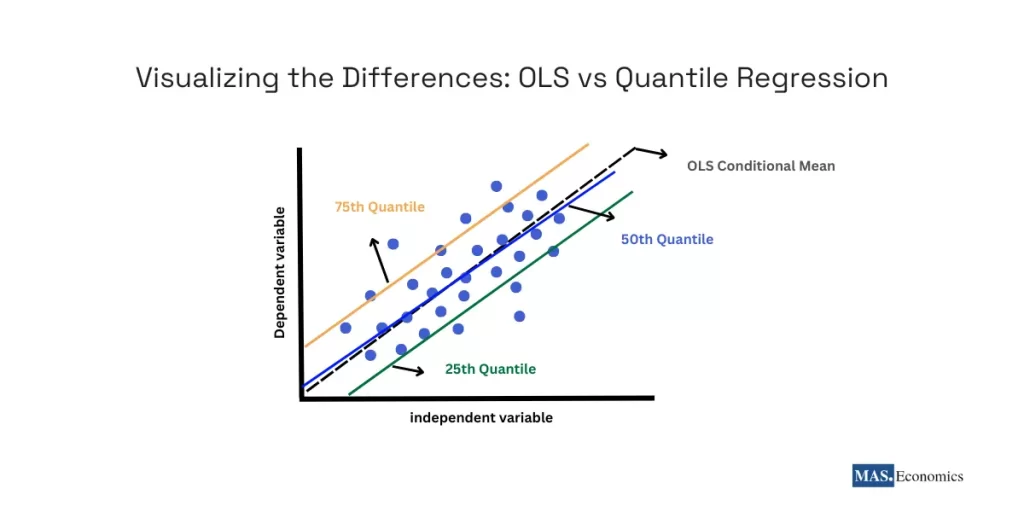
In the illustration , the OLS regression line captures the conditional mean, while quantile regression lines represent different quantiles of the dependent variable (e.g., 25th, 50th, and 75th quantiles). These lines reveal how the relationships between variables differ across various parts of the distribution.
Addressing Outliers and Data Irregularities
OLS minimizes squared residuals, making it highly sensitive to outliers. A few extreme values can disproportionately influence the regression line, leading to biased estimates. Quantile regression, by contrast, minimizes absolute residuals, which reduces the influence of outliers. This robustness makes quantile regression particularly suitable for datasets with skewed distributions or heavy-tailed variables, such as income, healthcare costs, or financial returns.
Handling Heteroskedasticity
OLS relies on the assumption of homoskedasticity, where the variance of errors is constant across observations. When this assumption is violated, OLS estimates become inefficient and unreliable. Quantile regression, however, naturally accommodates heteroskedasticity by modeling variable relationships across different quantiles. For example, it can show that the variability of healthcare costs increases for high-risk patients, even if the mean remains stable.
Flexibility with Non-Normal Data
Another critical limitation of OLS is its reliance on the assumption that residuals follow a normal distribution. Quantile regression eliminates this requirement, making it a more flexible tool for analyzing datasets that exhibit skewness, kurtosis, or other deviations from normality. This flexibility is particularly advantageous when analyzing financial returns, income distributions, or environmental data, where non-normal patterns are the norm rather than the exception.
Interpretation of Results
OLS provides a single coefficient estimate for each independent variable, reflecting its average effect. Quantile regression, on the other hand, generates a range of coefficients for different quantiles, revealing how the relationship between variables evolves across the distribution. For instance, the impact of advertising expenditure on sales might be more pronounced for high-spending customers (upper quantiles) than for low-spending ones (lower quantiles).
A Comparative Summary: OLS vs. Quantile Regression
Below is a comparison table that highlights the differences between OLS and quantile regression:
| Feature | Ordinary Least Squares (OLS) | Quantile Regression |
|---|---|---|
| Focus | Estimates the conditional mean | Estimates specific quantiles of the conditional distribution (e.g., median, quartiles). |
| Sensitivity to Outliers | Highly sensitive to outliers | Robust to outliers due to absolute residual minimization. |
| Handling Heteroskedasticity | Assumes constant variance | Handles heteroskedasticity by modeling variable effects across the distribution. |
| Distribution Assumptions | Requires normally distributed residuals | Does not require distributional assumptions. |
| Data Insights | Captures the “average” relationship | Captures heterogeneity by analyzing different parts of the distribution. |
| Applications | Suitable for symmetric and homogeneous data | Suitable for skewed, heteroskedastic, or heavy-tailed data. |
| Robustness | Less robust to data irregularities | Robust to skewness, non-normality, and extreme values. |
|
||
By addressing the limitations of OLS and offering a more comprehensive view of data relationships, quantile regression has become an essential tool for researchers analyzing complex and heterogeneous datasets.
Applications in Econometrics
Quantile regression is a versatile tool with wide-ranging applications in econometrics, enabling researchers to uncover insights that traditional regression methods often overlook. By analyzing how relationships vary across the conditional distribution of the dependent variable, quantile regression offers a more nuanced understanding of economic phenomena. Below are key areas where this method has proven particularly valuable.
Income Inequality and Wage Analysis
Quantile regression provides a deeper understanding of wage disparities by revealing how predictors influence different segments of the income distribution. For instance:
Example: In wage studies, quantile regression can show that the gender wage gap is relatively small at the lower end of the income spectrum but widens significantly for higher earners, offering critical insights for addressing inequality in high-income professions.
Healthcare Cost Modeling
Healthcare expenditures often exhibit extreme variability, with a small percentage of patients incurring disproportionately high costs. Quantile regression is particularly effective in this context.
Example: Quantile regression can identify that chronic conditions and advanced age are dominant drivers of costs at the upper quantiles of healthcare spending, helping insurers design targeted interventions for high-cost patients.
Financial Risk and Asset Pricing
In finance, quantile regression provides a robust framework for understanding the distribution of returns and risks.
Example: Quantile regression reveals that during market crises, macroeconomic shocks disproportionately affect the lower quantiles of stock returns, helping portfolio managers mitigate downside risk.
Environmental and Energy Economics
Environmental and energy data often exhibit heteroskedasticity and extreme values, making them ideal for quantile regression analysis.
Example: Quantile regression can model peak energy demand during extreme weather conditions, providing insights that help energy providers plan for high-demand scenarios.
By capturing variability and heterogeneity across these domains, quantile regression proves itself as a powerful tool for nuanced economic analysis.
Advantages of Quantile Regression in Complex Data Analysis
Quantile regression offers distinct advantages over traditional regression techniques, making it an indispensable tool for analyzing complex datasets. These advantages stem from its ability to handle heterogeneity, robustness to outliers, and flexibility in capturing relationships across the conditional distribution of the dependent variable.
Addressing Heteroskedasticity
Quantile regression excels in handling heteroskedasticity, where the variance of errors changes across observations. Unlike OLS, which assumes constant variance, quantile regression reveals how the relationship between variables evolves at different levels of the dependent variable.
Example: In financial markets, quantile regression identifies how interest rates influence stock returns differently during periods of high versus low market volatility, providing insights for more effective risk management.
Robustness to Outliers
Quantile regression minimizes absolute residuals, reducing the undue influence of extreme values that often distort OLS estimates.
Example: In income distribution studies, quantile regression ensures that high-income earners do not distort the analysis, allowing researchers to focus on more accurate determinants of wage disparities.
Capturing Data Heterogeneity
Many real-world datasets exhibit heterogeneity, where relationships vary across different groups or levels of the dependent variable. Quantile regression captures this heterogeneity, offering a detailed view of how predictors affect different segments of the population.
Example: In housing markets, quantile regression shows that location has a stronger impact on high-priced properties than on low-priced ones, enabling developers to make more informed investment decisions.
Flexibility in Non-Normal Data
Quantile regression does not rely on normality assumptions, making it highly adaptable for analyzing datasets that exhibit skewness or other irregular patterns.
Example: In energy consumption studies, quantile regression effectively captures how extreme weather events impact peak usage, even when data distributions are skewed.
Providing Comprehensive Insights
Quantile regression’s ability to estimate relationships at multiple quantiles provides a fuller picture of how variables interact across the spectrum of outcomes.
Example: In consumer behavior studies, quantile regression reveals that advertising has a larger impact on high-spending consumers, helping businesses optimize their marketing strategies.
By addressing these challenges, quantile regression empowers researchers and policymakers to extract meaningful insights from complex datasets, ensuring more reliable and impactful decision-making.
Conclusion
Quantile regression extends the scope of traditional econometric analysis by capturing the full conditional distribution of the dependent variable, not just the mean. By focusing on quantiles, it reveals variations across the distribution, addressing heterogeneity, outliers, and non-uniform error structures that standard methods may miss.
Whether analyzing income disparities, healthcare costs, or financial risk, quantile regression provides detailed insights into complex data patterns. Its ability to handle diverse and dynamic systems makes it a valuable tool for understanding relationships in economic and financial data.
FAQs:
What is quantile regression, and why is it used in econometrics?
Quantile regression is a method that analyzes the relationship between independent variables and specific quantiles of a dependent variable’s distribution. It is used to uncover how these relationships vary across different parts of the distribution, providing insights into heterogeneity that traditional regression methods, like OLS, may miss.
How does quantile regression handle outliers and skewed data?
Quantile regression minimizes absolute residuals, making it robust to outliers and effective in analyzing skewed or heavy-tailed data. This robustness ensures that extreme values do not disproportionately influence the results.
Why is quantile regression important for analyzing heterogeneity?
Quantile regression reveals how relationships between variables differ across various segments of the dependent variable’s distribution. For instance, it can show how education impacts wages differently for low-income versus high-income earners, offering a detailed view of heterogeneity in the data.
What are the practical applications of quantile regression in economics?
Quantile regression is widely applied in areas such as income inequality analysis, healthcare cost modeling, and financial risk assessment. For example, it can identify drivers of high healthcare costs or evaluate the effect of economic policies on income distribution across different population segments.
How does quantile regression differ from Ordinary Least Squares (OLS)?
While OLS focuses on estimating the average relationship between variables, quantile regression analyzes these relationships at different points in the dependent variable’s distribution. This allows it to capture nuances and variability that OLS may overlook.
Thanks for reading! Share this with friends and spread the knowledge if you found it helpful.
Happy learning with MASEconomics















